(一) 关于投资者无差异曲线的论述
对于一个特定的投资者,给定一个证券组合,根据该投资者的风险满意程度可以得到一系列满意程度相同的证券组合,并将这些证券组合所对应的均值和方差组合表示在均值—方差平面上,将这些点连接所得到的平滑曲线就是该投资者的无差异曲线。我们可以将无差异曲线所代表的满足程度(效用)看作均值和标准差的函数,即 ,同时托宾认为无差异曲线必定有一定的曲率,且呈凸状。无差异曲线如下图所示:
对于一个特定的投资者,给定一个证券组合,根据该投资者的风险满意程度可以得到一系列满意程度相同的证券组合,并将这些证券组合所对应的均值和方差组合表示在均值—方差平面上,将这些点连接所得到的平滑曲线就是该投资者的无差异曲线。我们可以将无差异曲线所代表的满足程度(效用)看作均值和标准差的函数,即 ,同时托宾认为无差异曲线必定有一定的曲率,且呈凸状。无差异曲线如下图所示:
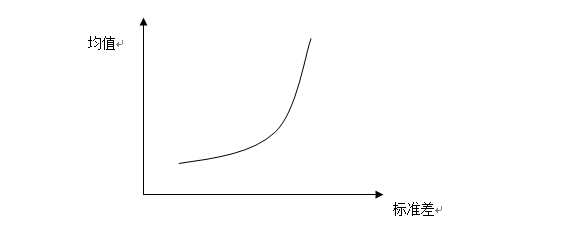
在上图中,无差异曲线上所代表的点都能给投资者带来相同的满意程度,但是对于不同的投资者,无差异曲线的形状也不相同。尽管不同的投资者面临不同的无差异曲线,但无差异曲线都具有以下几个特点:
1、 每条无差异曲线都是由左向右向上弯曲的曲线。
2、同一条无差异曲线上的组合给投资者带来的满意程度相同。
3、不同无差异曲线上的组合给投资者带来的满意程度不同。
4、每个投资者的无差异曲线都有无数条,并且这些无差异曲线在均值—方差平面上是不相交的。
5、无差异曲线的位置越高,其给投资者带来的满意程度也就越高。
6、无差异曲线的弯曲程度反映了投资者的风险承受能力。
(二) 最优资产组合的确定
托宾认为,投资者最优风险资产组合的确定应该是其无差异曲线与风险资产组合有效边界的切点。如下图所示:
1、 每条无差异曲线都是由左向右向上弯曲的曲线。
2、同一条无差异曲线上的组合给投资者带来的满意程度相同。
3、不同无差异曲线上的组合给投资者带来的满意程度不同。
4、每个投资者的无差异曲线都有无数条,并且这些无差异曲线在均值—方差平面上是不相交的。
5、无差异曲线的位置越高,其给投资者带来的满意程度也就越高。
6、无差异曲线的弯曲程度反映了投资者的风险承受能力。
(二) 最优资产组合的确定
托宾认为,投资者最优风险资产组合的确定应该是其无差异曲线与风险资产组合有效边界的切点。如下图所示:
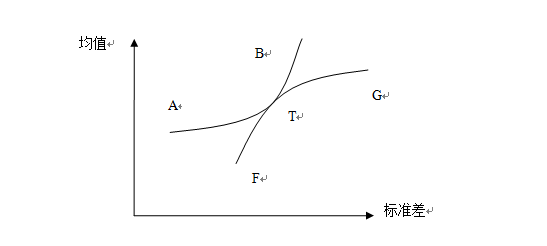
由上图所示,无差异曲线AB与有效边界FG的切点T,就是投资者最优的风险资产组合。因为只有在这一点投资者才能得到最大满足程度的资产组合,如果无差异曲线高于有效边界线,投资者在既定的财富约束下无法达到如此高的满足程度;如果无差异曲线与有效边界线相交,则投资者还没有达到既定约束水平下的最高满足程度,因此两者的切点才是投资者的最优风险组合。
(三) 纳入无风险资产的最优资产组合
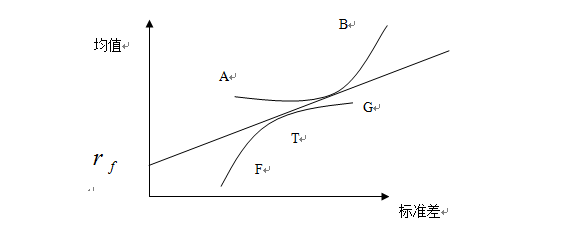
托宾认为,在纳入无风险资产后,投资者的有效边界组合就会发生改变,所有的有效组合都在由一条通过无风险收益率并与马克维兹有效边界相切的直线中,如下图所示。其中切点T就是最优的风险资产组合,直线 T以及T点的右半部分就是纳入无风险资产后的有效边界组合。
(三) 纳入无风险资产的最优资产组合
托宾认为,在纳入无风险资产后,投资者的有效边界组合就会发生改变,所有的有效组合都在由一条通过无风险收益率并与马克维兹有效边界相切的直线中,如下图所示。其中切点T就是最优的风险资产组合,直线 T以及T点的右半部分就是纳入无风险资产后的有效边界组合。
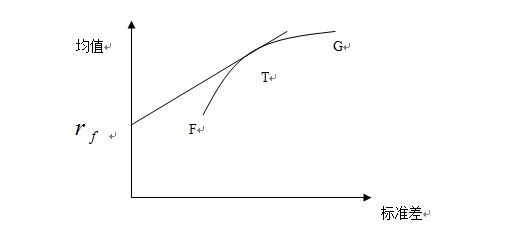
这样投资者的最优组合选择问题可以分为以下两个步骤:第一步,投资者先选择最优的风险投资组合,这一风险投资组合在马克维兹有效边界上,而通过无风险收益率并与有效边界相切的直线的切点就是最优风险资产组合,连接无风险利率和切点的直线就是投资者面临的有效组合的集合,同时投资者在选择这一最优风险资产组合时是不考虑他的风险规避度的;第二步,每个投资者在自己风险规避度和财富的约束下都会形成一个基于均值和方差的无差异曲线,同时投资者会将自己所拥有的财富在无风险利率和最优风险组合之间进行分配,这一最优组合就是上述无差异曲线和有效组合的切点。如下图所示:
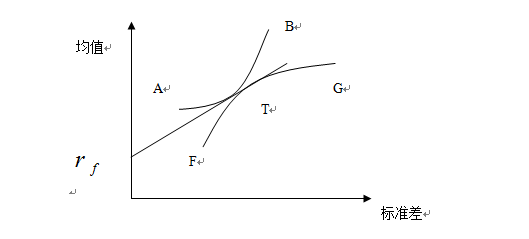
在上图中,无差异曲线与有效组合的切点在最有风险资产组合的左边,说明投资者不存在卖空行为,投资者只是将自己的财富在无风险利率和最有风险资产组合之间进行分配,无差异曲线与有效组合的切点就是投资者的最优资产组合。
在下图中,无差异曲线与有效组合的切点在最有风险资产组合的右边,说明投资者存在卖空行为,投资者先以无风险利率借入一定数量的资金,然后将自己所有的财富全部投资于最优风险资产组合。
在下图中,无差异曲线与有效组合的切点在最有风险资产组合的右边,说明投资者存在卖空行为,投资者先以无风险利率借入一定数量的资金,然后将自己所有的财富全部投资于最优风险资产组合。
因此,托宾将投资者的资产组合决策分解成了两个步骤,首先是最优风险资产组合的选择,其次是投资者最优投资组合的选择,并且这两个选择是互相独立的,这一结论也叫做两基金分离定理。




